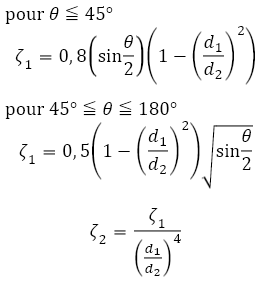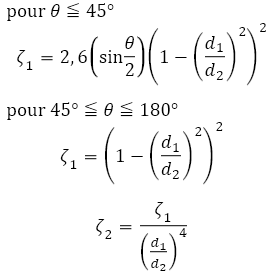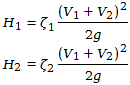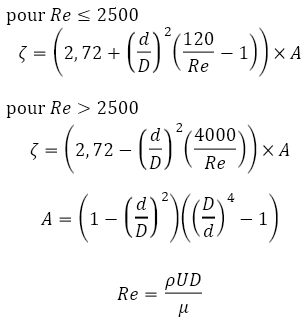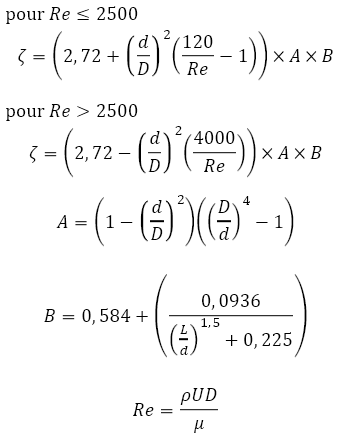Coefficients de perte de charge

Les pertes de charge dans les tuyauteries de transfert de fluide sont évaluées en appliquant la relation de Darcy. Cette relation fait appel aux caractéristiques de la tuyauterie elle même, par sa longueur (L) et son diamètre (D), et à des coefficients de perte de charge singulières (ζ dans la littérature européenne, K dans la littérature nord américaine), caractéristiques des accessoires de tuyauterie (vannes, clapets, coudes, changements de diamètre, ...). Différentes manières de tenir compte des pertes de charge singulières:

Longueur équivalente

 L'usage, à l'époque où l'absence de calculateurs rendaient les calculs numériques fastidieux, était de représenter les pertes de charge singulières des accessoires de tuyauterie par des longueurs équivalentes de tuyauterie de même diamètre. Celles-ci peuvent être ajoutées aux longueurs réelles de tuyauterie. Une simple abaque donnant la perte de charge au mètre linéaire suffit pour obtenir un résultat.
La critique qui est faite à cette méthode est que les longueurs équivalentes étant généralement déterminées expérimentalement en régime d'écoulement turbulent, conduisent à une surévaluation de la perte de charge lorsque le régime d'écoulement est laminaire. Cependant cette méthode possède encore ses partisans, préférant faire une erreur par excès plutôt que par défaut.

Coefficients de perte de charge

De nombreuses compilations de coefficients de perte de charge "génériques" sont disponibles. La plupart sont issus d'un document  de la Sté Crane, Flow of fluids Technical paper 410,  dont la première édition paru en 1942 et qui fut réédité à de nombreuses reprises. Une synthèse des informations importantes est disponible en téléchargement libre sur le site de la société Crane Nuclear.
Un autre ouvrage de référence est le Mémento des pertes de charge de I.E. Idel'Cik, initialement publié en russe et dont une traduction française est disponible à la vente.
L'idéal est en fait d'utiliser les caractéristiques de perte de charge fournies par les fournisseurs de chacun des éléments en place. Celles-ci peuvent être exprimées sous la forme de courbes, de coefficients de perte de charge, ou de coefficients de débit Cv pour les vannes et les clapets. La conversion des valeurs de Cv peut être faite en utilisant la relation suivante:
avec Dmm: diamètre nominal de raccordement en millimètre

Méthode dite 2K (W. Hooper)

La critique qui est faite aux coefficients de perte de charge génériques, est de ne pas tenir compte du Reynolds de l'écoulement traversant l'obstacle, et d'être généralement constant quel que soit le diamètre.
William Hooper proposa en 1981 (The two K method predicts head losses in pipe fittings - Chem. Eng. Aug. 17, 1981) une formulation faisant appel à deux nouveaux coefficients K1 et K∞. Le coefficient de perte de charge est alors calculé par la relation suivante:
avec Din: diamètre nominal de raccordement en pouce

Avec cette formulation, K₁ est prépondérant pour les Re faibles (régime laminaire) tandis que K_∞ devient prépondérant pour les Re élevés (régime turbulent).

Méthode dite 3K (R. Darby)

Ron Darby proposa en 1999 une amélioration de la méthode 2K de Hooper en introduisant un troisième paramètre K_d pour mieux représenter les résultats expérimentaux. Le coefficient de perte de charge est calculé par la relation suivante:

Coefficients de pertes de charge

Eléments de tuyauterie

	Coefficient de perte de charge ζ
Coudes à 90 deg soudés	d'après Crane r/d 1 1,5 2 4 6 8 ζ 0,45 0,3 0,25 0,2 0,25 0,35 Leq 20D 14D 12D 14D 17D 24D r/d 10 12 14 16 20 ζ 0,4 0,45 0,5 0,5 0,6 Leq 30D 34D 38D 42D 50D paramètres 2K (Hooper) r/d 1 K1 800 K∞ 0,25 ζ @ Re=100000 0,3-0,5 paramètres 3K (Darby) r/d 1 1,5 2 4 6 K1 800 800 800 800 800 K∞ 0,091 0,071 0,056 0,066 0,075 Kd 4,0 4,2 3,9 3,9 4,2 Pour les angles différents de 90 deg,, appliquer le coefficient de correction lu sur la courbe ci-contre, au coefficient de perte de charge du coude à 90 deg déterminé par l'une des méthodes ci dessus.
Coudes à extrémités filetées Leq=30D Leq=16D Leq=50D
	Coude 90 deg à onglet K1 K∞ (2K) K∞ (3K) Kd 1 raccord 90 deg 1000 1,15 0,27 4,0 2 raccords 45 deg 800 0,35 0,068 4,1 3 raccords 30 deg 800 0,30 0,035 4,2 4 raccords 22,5 deg 800 0,27 5 raccords 18 deg 800 0,25 Coude 45 deg à onglets paramètres Hooper et Darby K1 K∞ (2K) K∞ (3K) Kd 1 raccord 45 deg 500 0,25 0,086 4,0 2 raccords 22,5 deg 500 0,15 0,052 4,0 Pour les angles différents de 90 deg, appliquer le coefficient lu sur la courbe ci-contre.
Réductions	L'indice 1 se réfère au plus petit diamètre, tandis que l'indice 2 se réfère au plus grand. Si le calcul de perte de charge fait appel à la vitesse du fluide dans les sections de plus grand diamètre, le coefficient ζ2 doit être utilisé. ζ2 = ζ1(d2/d1)4 formules pour convergents (Crane): $\text{pour }θ≦45°$ $${ζ}_{1}=0,8\left(\sin{\frac{θ}{2}}\right)\left(1-{\left(\frac{{d}_{1}}{{d}_{2}}\right)}^{2}\right)$$ $\text{pour }45°≦θ≦180°$ $${ζ}_{1}=0,5\left(1-{\left(\frac{{d}_{1}}{{d}_{2}}\right)}^{2}\right)\sqrt{\sin{\frac{θ}{2}}}$$ $${ζ}_{2}=\frac{{ζ}_{1}}{{\left(\frac{{d}_{1}}{{d}_{2}}\right)}^{4}}$$
Augmentations de diamètre	L'indice 1 se réfère au plus petit diamètre, tandis que l'indice 2 se réfère au plus grand. Si le calcul de perte de charge fait appel à la vitesse du fluide dans les sections de plus grand diamètre, le coefficient ζ2 doit être utilisé. ζ2 = ζ1(d2/d1)4 formules pour divergents (Crane): $\text{pour }θ≦45°$ $${ζ}_{1}=2,6\left(\sin{\frac{θ}{2}}\right)\left(1-{\left(\frac{{d}_{1}}{{d}_{2}}\right)}^{2}\right)^{2}$$ $\text{pour }45°≦θ≦180°$ $${ζ}_{1}=\left(1-{\left(\frac{{d}_{1}}{{d}_{2}}\right)}^{2}\right)^{2}$$ $${ζ}_{2}=\frac{{ζ}_{1}}{{\left(\frac{{d}_{1}}{{d}_{2}}\right)}^{4}}$$
Tés	δ=45deg δ=90deg V1/Vtot ζ1 ζ2 ζ1 ζ2 0 0,9 0,04 0,96 0,05 0,2 0,66 -0,06 0,88 -0,08 0,4 0,47 -0,04 0,89 -0,04 0,6 0,33 0,07 0,96 0,07 0,8 0,29 0,2 1,1 0,21 1 0,35 0,33 1,29 0,35 ζ1 représente de coefficient de perte de charge pour le fluide prenant la bifurcation, ζ2 représente de coefficient de perte de charge pour le fluide allant en ligne droite, et ils se réfèrent au débit total entrant dans le té. $${H}_{1}={ζ}_{1}\frac{{\left({V}_{1}+{V}_{2}\right)}^{2}}{2g}$$ $${H}_{2}={ζ}_{2}\frac{{\left({V}_{1}+{V}_{2}\right)}^{2}}{2g}$$
Tés	δ=45deg δ=90deg V1/Vtot ζ1 ζ2 ζ1 ζ2 0 -0,09 0,05 -1,04 0,06 0,2 -0,37 0,17 -0,4 0,18 0,4 0 0,18 0,1 0,3 0,6 0,22 0,05 0,47 0,4 0,8 0,37 -0,2 0,73 0,5 1 0,38 -0,57 0,92 0,6 ζ1 représente de coefficient de perte de charge pour le fluide prenant la bifurcation, ζ2 représente de coefficient de perte de charge pour le fluide allant en ligne droite, et ils se réfèrent au débit total entrant dans le té.
Orifice mince	formules pour calculateur (Hooper): $\text{pour }Re\leq2500$ $$ζ=\left(2,72+\left(\frac{d}{D}\right)^{2}\left(\frac{120}{Re}-1\right)\right)×A$$ $\text{pour }Re≻2500$ $$ζ=\left(2,72-\left(\frac{d}{D}\right)^{2}\left(\frac{4000}{Re}\right)\right)×A$$ $$A=\left(1-{\left(\frac{d}{D}\right)}^{2}\right)\left({\left(\frac{D}{d}\right)}^{4}-1\right)$$ $$Re=\frac{ρUD}{μ}$$ Source: Calculate Head Loss Caused by Change in Pipe Size - Chem. Eng. Nov. 7, 1988
Orifice épais (L/d<5)	Si L/d >5, le considérer comme la succession d'une contraction brusque (θ=180 deg), une tuyauterie de diamètre d, et une augmentation brusque de diamètre. formules pour calculateur (Hooper): $\text{pour }Re\leq2500$ $$ζ=\left(2,72+\left(\frac{d}{D}\right)^{2}\left(\frac{120}{Re}-1\right)\right)×A×B$$ $\text{pour }Re≻2500$ $$ζ=\left(2,72-\left(\frac{d}{D}\right)^{2}\left(\frac{4000}{Re}\right)\right)×A×B$$ $$A=\left(1-{\left(\frac{d}{D}\right)}^{2}\right)\left({\left(\frac{D}{d}\right)}^{4}-1\right)$$ $$B=0,584+\left(\frac{0,0936}{{\left(\frac{L}{d}\right)}^{1,5}+0,225}\right)$$ $$Re=\frac{ρUD}{μ}$$ Source: Calculate Head Loss Caused by Change in Pipe Size - Chem. Eng. Nov. 7, 1988
Entrée de tuyauterie (sortie de réservoir) ζ = 0,78 r/d ζ 0 0,5 0,02 0,28 0,04 0,24 0,06 0,15 0,1 0,09 >0,15 0,04
Débouché de tuyauterie (entrée de réservoir) ζ = 1,0 ζ = 1,0 ζ = 1,0

Vannes et clapets

	Coefficient de perte de charge ζ
Vanne à soupape droite (globe valve)	si pas de réduction de la section de passage au siège du clapet: Diam nominal 1" 2" 4" 8" >16" ζ 7,5 6,5 5,4 4,8 4,1 Leq 340D Paramètres Hooper et Darby 2K 3K K1 1500 1500 K∞ 4 1,7 Kd - 3,6 ζ @ Re=100000 4,5-8 si la section de passage est réduite au siège du clapet (clapet réduit ou vanne partiellement fermée), multiplier le coefficient par la correction ci-contre
Vanne à soupape en équerre	si pas de réduction de la section de passage au siège du clapet: Diam nominal 1" 2" 4" 8" >16" ζ 3,3 2,9 2,4 2,1 1,8 Leq 150D Paramètres Hooper et Darby 2K 3K K1 1000 1000 K∞ 2 0,69 Kd - 4 ζ @ Re=100000 2-4 2-3,5
Vanne à soupape en Y	Diam nominal 1" 2" 4" 8" >16" ζ 1,2 1,0 0,9 0,8 0,7 Leq 55D Paramètres Hooper et Darby 2K 3K K1 950 K∞ 0,25 Kd - 4 ζ @ Re=100000 0,7-1,3
Vanne à opercule (gate valve)	Les vannes à opercule sont disponibles avec deux types d'orifice:  - standard ou conventionel; l'orifice est plus petit que la section nominale du raccordement à la tuyauterie. Une zone de rétrécissement fait la liaison entre les deux aussi bien pour l'entrée que pour la sortie. Moins coûteuses, elles seront préférée en l'absence de contrainte de perte de charge.  - full bore ou passage intégral; l'orifice de passage est exactement du même diamètre que le raccordement à la tuyauterie. d'après Crane pour un écoulement turbulent ζstd=ζint(d2/d1)4 + ζconv + ζdiv standard passage intégral DN d2 (in) d1 (in) θ (deg) ζ Leq (m) ζ Leq (m) 1 ¾ 6 0,72 1 0,2 0,2 1½ 1 12 1,69 3 0,18 0,3 2 1½ 10 0,8 2 0,17 0,4 3 2 15 1,57 6 0,16 0,6 4 3 15 0,82 5 0,14 0,9 6 4 21 1,77 16 0,13 1,3 8 6 21 0,88 12 0,12 1,7 10 8 19 0,54 10 0,12 2,1 12 10 17 0,39 9 0,11 2,6 14 12 7 0,18 5 0,11 2,8 16 14 10 0,24 7 0,11 3,2 18 16 10 0,21 7 0,1 3,8 20 18 9 0,19 7 0,1 4,1 24 20 15 0,36 18 0,1 4,9 Paramètres Hooper et Darby 2K 3K d1/d2 =1 d1/d2 =0,8 d1/d2 =1 K1 300 1000 300 K∞ 0,15 0,25 0,037 Kd - - 3,9 Si la vanne est partiellement ouverte, le coefficient de perte de charge doit être multiplié par le facteur de correction lu sur le graphique ci-contre.
Vanne papillon (butterfly valve)	Les vannes papillon les plus classiques sont dites centrées parce que le papillon est symétrique et sont axe de rotation est placé exactement sur l'axe de la vanne. Dans le but d'améliorer l'étanchéité du papillon fermé, certains constructeurs proposent des vannes ayant jusqu'à trois "excentrations":  - l'axe de rotation est déplacé à l'arrière du papillon  - l'axe de rotation est déplacé en dehors de l'axe de la vanne  - le siège sur lequel vient reposer le papillon n'est pas symétrique Ces différences de conception conduisent à des variations significatives du coefficient de perte de charge. Papillon centré d'après catalogues fournisseurs DN 2-3" 4" 6" 8" 10-16" 18-24" ζ 0,8 0,65 0,45 0,35 0,25 0,20 Leq 45D 40D 30D 25D 20D 15D paramètres Hooper 2K K1 800 K∞ 0,25 Kd - ζ @ Re=100000 0,5-0,3 Papillon à double excentration d'après Crane pour régime turbulent Diam nominal 2 - 8" 10-14" >16" ζ 1,2 0,68 0,52 Leq 74D 52D 43D Papillon à triple excentration d'après catalogues fournisseurs DN 3" 4" 6" 8" 10-16" 18-24" ζ 7 5 3 2,5 1,5 1,2 Leq 430D 300D 200D 160D 120D 100D Si le papillon est partiellement fermé, le coefficient de perte de charge doit être multiplié par le facteur de correction lu sur le graphique ci-contre. Noter que le mouvement du papillon étant différent selon qu'il est centré ou excentré, la correction est elle aussi différente.
Vanne à boule (ball valve)	Les vannes à boule sont disponibles avec deux types d'orifice:  - standard ou conventionel; l'orifice est plus petit que la section nominale du raccordement à la tuyauterie. Une zone de rétrécissement fait la liaison entre les deux aussi bien pour l'entrée que pour la sortie.  - full bore ou passage intégral; l'orifice de la boule est exactement du même diamètre que le raccordement à la tuyauterie. d'après Crane pour un écoulement turbulent standard intégral DN d2 (in) d1 (in) θ (deg) ζ Leq (m) ζ Leq (m) 1 ¾ 6 0,41 0,4 0,09 0,1 1½ 1 12 1,17 2 0,09 0,2 2 1½ 10 0,51 1,3 0,08 0,2 3 2 15 1,16 5 0,075 0,3 4 3 15 0,58 3 0,07 0,4 6 4 21 1,43 14 0,065 0,6 8 6 21 0,68 9 0,06 0,8 10 8 19 0,39 7 0,055 1 12 10 17 0,27 6 0,055 1,3 14 12 7 0,10 3 0,05 1,4 16 14 10 0,14 4 0,05 1,5 18 16 10 0,12 4 0,05 1,8 20 18 9 0,11 4 0,05 2 24 20 15 0,25 12 0,05 2,4 Paramètres Hooper et Darby pour tous régimes d'écoulement 2K 3K d1/d2 =1 d1/d2 =0,8 d1/d2 =1 K1 300 1000 300 K∞ 0,15 0,25 0,037 Kd - - 3,9 Effet de l'angle d'ouverture Pour une vanne partiellement fermée, il convient de corriger le coefficient de perte de charge en le multipliant par le facteur lu sur la courbe ci-contre.
Clapet anti retour à disque basculant (tilting check valve)	α = 5 deg d'après Crane pour régime turbulent Diam nominal 1" 2" 4" 8" 10-14" >16" ζ 0,9 0,8 0,6 0,6 0,4 0,2 Leq 40D 30D 20D α = 15 deg Diam nominal 1" 2" 4" 8" 10-14" >16" ζ 2,6 2,3 1,9 1,7 1,2 0,7 Leq 120D 90D 60D
Clapet anti retour à battant (swing check valve)	Diam nominal 1" 2" 4" 8" 10-14" >16" ζ 1,1 1,0 0,8 0,7 0,65 0,6 Leq 50D
Clapet anti retour à clapet (lift check valve)	d1/d2 = 1 Diam nominal 1" 2" 4" 8" 10-14" >16" ζ 13 12 10 9 8 7 Leq 600D d1/d2 = 0,7 Diam nominal 1" 2" 4" 8" 10-14" >16" ζ 54 50 42 38 33 29 Leq 2500D

Echangeurs

Coté calandre pas carré - tubes allignés	d'après Kern (1950) la perte de charge coté calandre est principalement due à la restriction de passage entre les tubes. Re = ρ.Umax.de⁄µf avec: Umax: vitesse maxi du fluide entre deux tubes adjacents de: diamètre équivalent à l'espace entre les tubes de = (4Cpx²-πd²)⁄πd Pour obtenir le coefficient de perte de charge  global de l'échangeur, multiplier le coefficient lu sur le graphe ci-joint par:  - le nombre de rang de tubes traversé par le fluide entre deux chicanes  - le nombre de fois où le faisceau est traversé (Nchicanes + 1) Si la viscosité du fluide est très sensible aux variations de température dans l'échangeur, Kern propose la correction suivante: multiplier le coefficient de perte de charge lu sur les courbes ci-jointes par:  - si Re<2100: 1,1(µt/µf)0,25  - si Re>2100: (µt/µf)0,14 avec: µt : viscosité du fluide à la température des tubes µf: viscosité du fluide à sa température La vitesse de référence est la vitesse maximale entre deux tubes adjacents. Pour ramener le coefficient à une vitesse de référence différente, le corriger par le carré du rapport des sections de passage: ζ2=ζ1(S2/S1)2
tubes en quinconce pas triangulaire (30°) pas carré (45°)
Coté intra-tubes	Appliquer la même méthode que pour les tuyauteries, sans oublier les coefficients de perte de charge pour les entrées et les débouchés (une entrée et un débouché pour chaque passe de tube). Cependant si l'échangeur est inclu dans un réseau dont la perte de charge sera évaluée globalement, calculer un coefficients de perte de charge pour le coté tubes par: ζech = (pζent + pζsort + f L/dt) (Dref/dt)4/ n2 avec: dt: diamètre interne des tubes Dref: diamètre de la tuyauterie prise comme référence pour l'évaluation du réseau L: longueur des tubes f: facteur de frottement pour Re dans les tubes n: nombre de tubes par passe p: nombre de passes coté tubes
Echangeur à tubes concentriques	La perte de charge dans l'espace annulaire se calcule comme celle d'une tuyauterie pour laquelle le diamètre est remplacé par un diamètre équivalent donné par: De = (D22- d12)/(D2 + d1) Pour tenir compte des entrées et sorties ajouter ζ=1,0 par épingle (un aller et un retour) Si l'échangeur est inclu dans un réseau dont la perte de charge sera évaluée globalement, calculer un coefficients de perte de charge pour le coté tubes par: ζech = (pζe/s + f L/De) (Dref/De)4 avec: p: nombre d'épingles ζe/s: coefficient pour les raccordements d'entrées et sorties (=1,0 d'après Kern) L: longueur développée de l'échangeur Dref: diamètre de la tuyauterie prise comme référence pour l'évaluation du réseau f: facteur de frottement pour Re dans l'espace annulaire des tubes
Serpentins	Le fluide en écoulement dans un serpentin subit une force centrifuge qui provoque au sein du liquide un mouvement tourbillonnant supplémentaire, qui n'existe pas dans un tube rectiligne. La perte de charge s'en trouve augmentée. De nombreuse sources proposent des corrections au facteur de frottement en tube rectiligne pour tenir compte de ce phénomène. Nous avons choisi ici d'appliquer cette correction à la longueur du tube du serpentin pour en faire une longueur équivalente Leq. Elle peut ainsi être ajoutée aux autres pertes de charge singulières du circuit. La plupart des études qui ont abouti à ce facteur de correction ont été menées sur des tubes lisses. On doit supposer que la même correction s'applique à un tube rugueux. D'après H. Ito Friction factors for turbulent flow in curved pipes, J. Basic Engng. Trans. ASME D 81 (1959) 123-124 Leq/L = (1+0,03(d/D)0,5)Re0,25/0,3164 D'après Crane Crane propose une démarche différente et fourni des coefficients de perte de charge pour coude à 90° de différentes courbures, et une relation pour les sommer et obtenir le coefficient correspondant à un serpentin à n coudes. Pour obtenir la courbe ci-contre, cette relation est transformée en: Leq/L = ((n-1)(π/8 x D/d + leq/2d) + leq/d)d/leq avec: Leq: longueur équivalente du serpentin leq: longueur équivalente d'un coude à 90° L: longueur déployée du tube du serpentin d: diamètre du coude ou du tube du serpentin n: nombre de coudes à 90° constituant le serpentin D: diamètre du serpentin r/d leq/d r/d leq/d 2 12 10 30 3 12 12 34 4 14 14 3 6 17 16 42 8 24 20 50