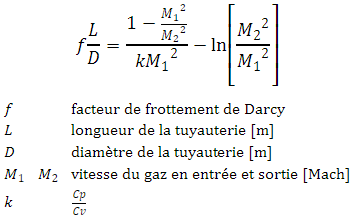Avertissement au visiteur!

Calcul des conditions d'écoulement d'un gaz dans une tuyauterie

Sommaire de la page:

Ecoulement sans échange de chaleur
Nombre de Mach
Profil de température sans échange de chaleur
Ecoulement isotherme
Logique de calcul
Variables et Unités

Voir aussi ...

Cette page détaille les équations utilisées dans la feuille de calcul "Tuyauterie gaz" du fichier ProcesssCalc

L'écoulement de gaz dans une tuyauterie présente les particularités suivantes:

Les frottements sur la paroi de la tuyauterie génèrent une perte de charge (diminution de la pression) progressive le long du parcours.
La diminution de pression le long de la tuyauterie provoque l'augmentation de la vitesse du gaz qui à son tour augmente la perte de charge. La variation de pression n'est donc pas linéaire en fonction de la longueur.
La vitesse du gaz ne peut dépasser une valeur dite critique, qui dépend de la nature du gaz. Cette vitesse correspond également à la vitesse du son dans ce même gaz.
Une fois cette vitesse critique atteinte, la pression ne peut plus décroître (une diminution de la pression aurait pour effet d'augmenter la vitesse qui est déjà maximum). Le débit est donc limité, et ne peut être augmenté que par l'augmentation de pression amont.
L'expansion du gaz étant due aux frottements contre la paroi, c'est une évolution irréversible (on ne peut pas inverser le phénomène de frottement pour retrouver l'état initial du gaz). Il y aura donc augmentation de l'entropie du gaz.
L'écoulement peut être de type adiabatique (sans échange de chaleur avec l'extérieur) ou isotherme (à température constante) ou encore polytropique (avec échange de chaleur conduisant à une augmentation ou une diminution de température), ce qui aura des conséquences différentes sur l'évolution de la masse volumique du gaz.
Si aucun échange de chaleur ne se produit avec l'extérieur, l'expansion du gaz sera isenthalpique (adiabatique mais non isentropique).

Ecoulement sans échange de chaleur

Relation de Fanno:

Equation de Fanno pour l'écoulement isenthalpique de fluides compressibles en régime sous-critique

f \frac{L}{D} = \frac{1}{k} (\frac{1}{{M_{1}}^{2}} - \frac{1}{{M_{2}}^{2}}) + \frac{k + 1}{2 k} \ln [\frac{{M_{1}}^{2} (1 + \frac{k - 1}{2} {M_{2}}^{2})}{{M_{2}}^{2} (1 + \frac{k - 1}{2} {M_{1}}^{2})}]

$\begin{array}{ll} f & facteur de frottement de Darcy \\ L & longueur de la tuyauterie [m] \\ D & diamètre de la tuyauterie [m] \\ M_{1} M_{2} & vitesse du gaz en entrée et sortie [Mach] \\ k & \frac{C p}{C v} \end{array}$

Variables et Unités

L'écoulement adiabatique du gaz dans une tuyauterie (Débit et profil de Pression) est solution de l'équation de Fanno:

Elle permet de calculer le profil de vitesses du gaz le long d'une tuyauterie en fonction des propriétés du gaz et des caractéristiques de la tuyauterie; les vitesses sont exprimées en nombre de Mach (M₁ en entrée et M₂ en sortie).

Nombre de Mach

Vitesse d'écoulement d'un gaz en nombre de Mach

M = \frac{F}{A} \frac{1}{P} \sqrt{\frac{z R T}{k M_{w}}}

$\begin{array}{ll} M & vitesse du gaz [Mach] \\ F & débit de gaz [kg╱s] \\ A & {section de passage [m}^{2}] \\ P & pression du gaz [Pa] \\ k & \frac{C p}{C v} \\ z & compressibilité du gaz \\ T & température [°K] \\ M_{w} & masse molaire du gaz [kg╱mole] \\ R & 8.3145 Pa·m^{3} ╱mole╱K \end{array}$

Variables et Unités

Le nombre de Mach est le rapport de la vitesse sur la vitesse du son dans le gaz. Il peut s'exprimer directement en fonction du débit et des pression et température du gaz.

Le nombre de Mach ne peut être supérieur à 1. Lorsqu'il atteint la valeur de 1 le long de la tuyauterie, le régime d'écoulement est dit "critique" ("choked flow" dans la littérature anglo-saxonne). La valeur de Mach=1 ne peut être atteinte qu'à l'extrémité de sortie de la tuyauterie.

Profil de température sans échange de chaleur

Température statique

Variation de température statique mesurée sur un fluide compressible en écoulement

\frac{T_{2}}{T_{1}} = \frac{1 + \frac{k - 1}{2} {M_{1}}^{2}}{1 + \frac{k - 1}{2} {M_{2}}^{2}}

$T_{1} T_{2}$	température statique du gaz en entrée et sortie [°K]
$M_{1} M_{2}$	vitesse du gaz en entrée et sortie [Mach]
$k$	$\frac{C p}{C v}$

Variables et Unités

L'énergie du gaz en écoulement se répartie entre son enthalpie et son énergie cinétique. Quand la vitesse du gaz augmente, son enthalpie ainsi que sa température diminuent. Ces variations d'enthalpie et de température, seulement dues à la variation de vitesse peuvent être temporaires; si le gaz retrouve sa vitesse initiale, il retrouvera sa température initiale s'il se comporte comme un gaz parfait.
On nomme "température de stagnation", la température du gaz au repos, et "température statique" la température mesurée du gaz en écoulement.

Les température et pression au point d'entrée sont renseignés. En écoulement adiabatique la température de sortie dépend du profil de pression, la section de passage étant supposée constante.

Ecoulement isotherme

Ecoulement isotherme de gaz dans une tuyauterie:

Relation pour l'écoulement isotherme d'un fluide compressible

f \frac{L}{D} = \frac{1 - \frac{{M_{1}}^{2}}{{M_{2}}^{2}}}{k {M_{1}}^{2}} - \ln [\frac{{M_{2}}^{2}}{{M_{1}}^{2}}]

Variables et Unités

L'écoulement isotherme du gaz dans une tuyauterie (Débit et profil de Pression) est solution de l'équation

Logique de calcul

Les données d'entrée sont:

Caractéristiques de la tuyauterie (Diamètre, Longueur, Rugosité)
Caractéristiques du gaz (Masse molaire, Cp/Cv, viscosité)
Conditions opératoires (Débit, Pression et température de la source, Pression en aval)

Sont calculés:

Reynolds aux conditions d'entrée
Le facteur de frottement est calculé par:

la relation de Poiseuille en régime laminaire

la relation de Churchill en régime turbulent

Oups!
La page que vous avez demandé n'existe pas encore ou n'existe plus !
Désolé
Vous pouvez retourner vers la
page d'accueil

Nombres de Mach pour l'entrée et la sortie (en considérant la pression aval comme pression de sortie de la tuyauterie). Si la valeur de Mach en sortie est >1, elle est forcée =1
La relation de Fanno est évaluée

Itérations:
La variable sélectionnée est ajustée par le solver pour satisfaire la relation de Fanno. Si au cours des itérations la valeur de Mach en sortie est >1, elle est forcée =1

Variables et Unités

Variable	Dimension	Unité SI
M: nombre de Mach	-	-
P: pression du fluide	ML^-1T^-2	N/m²
V: volume du fluide	L³	m³
T: température du fluide		K
L: longueur de la tuyauterie	L	m
D: diamètre de la tuyauterie	L	m
F: débit du fluide	MT^-1	kg/sec
U: vitesse du fluide	LT^-1	m/sec
f: facteur de frottement de Darcy	-	-
k = Cp/Cv: rapport des capacités calorifiques à pression constante (Cp) et à volume constant (Cv)	-	-
Mw: masse molaire du gaz	M	kg
z:	-	-
e: rugosité de la tuyauterie	L	m
A: aire de passage	L²	m²
R: constante des gaz parfaits (8,3145 Pa.m³/mole/°K)
M: masse L: longueur T: temps

Votre avis est précieux pour améliorer ce site.

Avez-vous trouvé cette page utile?